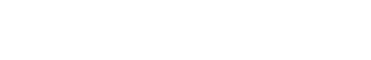ELASTIC SYSTEM FOR SCREENERS AND FEEDERS

What are the elastic elements used in screeners

As an elastic system element in screens and , it is possible use elements in which spiral steel springs, rubber supports and rubber elements are placed inside a special structure. Steel springs are the most common and the most economic elastic system elements in screens and 

Advantages of rubber supports over steel springs:
1.As the spring ratio of rubber springs varies according to the load, a constant natural frequency with varying loads is ensured, which in turn allows the provision of good isolation.
2.High load-bearing capacities.
3.Since they have a lower spring ratio in the horizontal when compared to the vertical, they provide good isolation in a horizontal direction
4.More efficient than steel springs in humid and corrosive environments.
5.Less noise generated.

The special vibration element shown on the right in Picture 1 provides high isolation in a lateral direction, along with a very low natural frequency, which allows the system to function in a more stable manner. Their ease of assembly permit them to be readily integrated into the system without the requirement for extra structures, being connected through their connection holes.

2.4.2 Spring Selection

Resonance is known to be an important problem in all dynamic systems, and so all  are designed to operate outside their resonance frequency, and this situation also affects the vibrating screen spring selection procedure. All screens are designed to run at 3 or 5 times the resonance frequency to protect the system and to ensure a uniform screening operation.
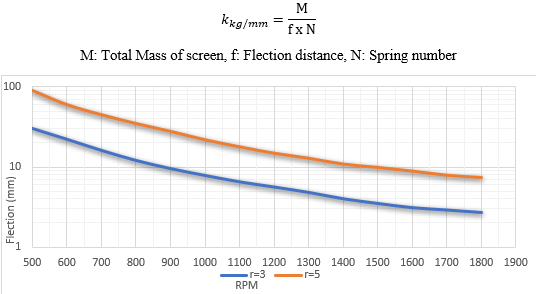
All springs are selected with a running condition of 3 or 5 times the resonance frequency with respect to this precondition. Diagram 8 below can be used to determine the spring constant (k) with respect to the formula:

2.4.3 Stroke & Eccentric Mass Weight Calculation

Traditional vibration and amplitude calculation methods are used in this step, although the resonance definition and calculation must be understood properly when calculating the stroke and eccentric mass.
Resonance, an object free to vibrate tends to do so at a specific rate referred to as the object's natural, or resonant, frequency (ωn) (This frequency depends on the size, shape and composition of the object). Such an object will vibrate strongly when subjected to vibration or regular impulses at a frequency equal to or very close to its natural frequency. This phenomenon is called resonance. Through resonance, a comparatively weak vibration in one object can cause a strong vibration in another.

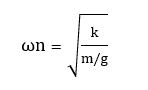
ωn : Natural frequency (Rad/sec)
k : Resultant spring constant (N/m)
m : Total mass of system (kg)
g : Gravitational acceleration (m/s2)

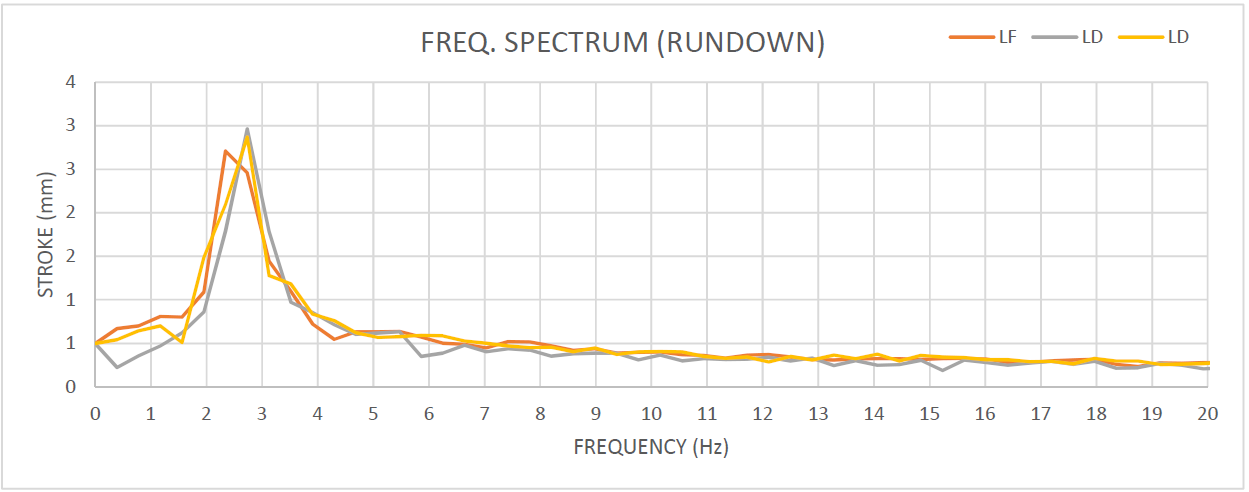
As an example of resonance, a motor that causes vibration in one part of a car causes vibration in another part of the vehicle. These vibrations occur when an object has a natural frequency that is equal to the frequency of the vibrations of the motor. Such objects are said to be “in resonance” with the motor. Resonance is observed in vibrating screens either in the run up or run down steps. When a motor’s rotational speed approaches the natural frequency of the screen in the run up and run down steps and comes to meet the critical frequency (diagram 9), the screen witnesses an aggressive vibration motion like an angry bull, with the motion being completely unpredictable and chaotic.

Mechanical resonance can produce vibrations that are strong enough to destroy the object in which they occur. For example, soldiers marching over a bridge can set up extreme vibrations at the bridge's natural frequency and shake it apart. For this reason, soldiers break step when crossing bridges. In 1940, strong winds at the Puget Sound Narrows, Tacoma, Washington, caused a suspension bridge to vibrate at its natural frequency and the bridge collapsed

Circular vibrating screens generally run with an 8 mm stroke, while horizontal vibrating screens run with a 16 mm stroke, and spring selection,  design and eccentric masses are defined and designed depending on these stroke values.

The amplitude of harmonically forced vibration is calculated using the formula below. As can be seen in this formula, amplitude is directly related to the eccentric forces exerted by eccentric masses, the natural frequency, the mass and spring constant, and the rotation of the system.

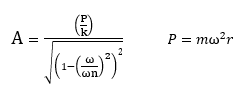
A : Amplitude of vibration (m)
P : Total eccentric force (N)
k : Spring constant (kg/m)
ω : Rotational speed (RPM)
ωn : Natural frequency (RPM)
m : Total eccentric mass (kg)
r : Eccentricity radius (m)

The spring selection procedure has been explained in an earlier step, so the only unknown in the equation is the amplitude and eccentric mass weight. Eccentric mass can be calculated easily with respect to the desired stroke value by this equation.

Important Note: Damping affects are disregarded in this calculation.